Kas yra Macaulay trukmė?
„Macaulay“ trukmė - tai laikas, per kurį investuotojas atgauna investuotus pinigus į obligaciją per kuponus ir grąžindamas pagrindinę sumą. Šis laikotarpis yra svertinis laikotarpio, kurį investuotojas turėtų ir toliau investuoti į vertybinius popierius, vidurkis, kad dabartinė investicijų pinigų srautų vertė atitiktų sumą, sumokėtą už obligaciją.
„Macaulay“ trukmė yra labai svarbus veiksnys, į kurį reikia atsižvelgti prieš perkant skolos priemonę. Tai gali labai padėti investuotojams rinktis iš įvairių rinkoje esančių fiksuotų pajamų vertybinių popierių rinkinių. Kaip visi žinome, obligacijų kainos yra atvirkščiai susijusios su palūkanų normomis. Investuotojai gerai suvokia, kurią obligaciją pirkti, ilgesnės ar trumpesnės trukmės, jei žino įvairių siūlomų kuponų obligacijų trukmę ir numatomą palūkanų normos struktūrą.
Macaulay trukmės formulė
Tai galima apskaičiuoti naudojant šią formulę:
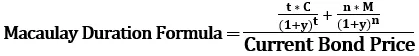

Kur,
- t = laikotarpis
- C = kupono mokėjimas
- y = derlius
- n = periodų skaičius
- M = branda
- Dabartinė obligacijų kaina = dabartinė pinigų srautų vertė
Macaulay trukmės apskaičiavimas su pavyzdžiu
Pažiūrėkime į Macaulay trukmės pavyzdį, kad ją geriau suprastume.
1 000 USD vertės obligacija moka 8% kupono palūkanų normą ir baigia galioti per ketverius metus. Kupono norma yra 8% per metus. Mokant pusmetį. Galime tikėtis, kad atsiras šie pinigų srautai.
- 6 mėnesiai: 40 USD
- 1 metai: 40 USD
- 1,5 metų: 40 USD
- 2 metai: 40 USD
- metų: 40 USD
- 3 metai: 40 USD
- 3,5 metų: 40 USD
- 4 metai: 1040 USD
Apskaičiuokite Macaulay trukmę
Sprendimas:
Turėdami aukščiau pateiktą informaciją, galime apskaičiuoti nuolaidos koeficientą. Norėdami nustatyti diskonto koeficientą, galime naudoti šią pusmečio palūkanų formulę. 1 / (1 + r) n, kur r yra kupono palūkanų norma, o n - sujungtų laikotarpių skaičius.
Nuolaidos koeficientas
Diskonto koeficientų apskaičiavimas 6 mėnesiams bus -

6 mėnesių nuolaidų koeficientai = 1 / (1 + 8% / 2)
Nuolaidos koeficientai = 0,9615
Panašiai galime apskaičiuoti 1–4 metų diskonto koeficientą.

Dabartinė pinigų srautų vertė
Dabartinė 6 mėnesių pinigų srauto vertė bus -

Dabar, norėdami gauti dabartinę pinigų srautų vertę, kiekvieno laikotarpio pinigų srautus turime padauginti iš atitinkamo diskonto koeficiento.
Dabartinė 6 mėnesių pinigų srautų vertė: 1 x 40 USD x 0,9615
Dabartinė pinigų srautų vertė = 38,46 USD
Panašiai galime apskaičiuoti dabartinę pinigų srautų vertę nuo 1 iki 4 metų.

Macaulay Trukmė
Macaulay trukmė bus apskaičiuota -

- Dabartinė obligacijų kaina = visų pinigų srautų PV 6 079,34
- „Macaulay“ trukmė = 6 079,34 USD / 1 000 USD = 6,07934
Norėdami išsamiai apskaičiuoti „Macaulay“ trukmę, galite kreiptis į pateiktą „Excel“ šabloną.
Trukmės naudojimo nuopelnai
Trukmė vaidina svarbų vaidmenį padedant investuotojams suprasti turimo fiksuotų pajamų vertybinių popierių rizikos veiksnį. Lygiai taip pat, kaip akcijų rizika matuojama nukrypstant nuo vidurkio arba paprasčiausiai išvedant vertybinių popierių beta versiją, rizika fiksuotų pajamų priemonėse yra griežtai įvertinta pagal Macaulay priemonės trukmę.
Suprasti ir palyginti „Macaulay“ priemonių trukmę gali būti ilgas kelias pasirenkant tinkamą jūsų fiksuotų pajamų portfelio tinkamumą.
Trukmės naudojimo nesėkmės
Trukmė yra geras apytiksliai kainų pokyčių obligacijų be pasirinkimo sandoriui, tačiau jis tinka tik nedideliems palūkanų normų pokyčiams. Palūkanų normos pokyčiams didėjant, obligacijų kainos ir pajamingumo santykio kreivumas tampa svarbesnis. Kitaip tariant, linijiniame kainos pokyčių įvertinime, pvz., Trukmėje, bus klaidų.
Tiesą sakant, obligacijų kainos ir pajamingumo santykis nėra tiesinis, o išgaubtas. Šis išgaubtumas rodo, kad skirtumas tarp faktinių ir apskaičiuotų kainų didėja, didėjant derliui. Tai yra, didėjanti numatomos kainos paklaida atsiranda dėl faktinio kainų kelio kreivumo. Tai vadinama išgaubtumo laipsniu.
Apatinė eilutė
Macaulay Trukmės žinios yra svarbiausios norint nustatyti būsimųjų pajamų iš fiksuotų pajamų priemonių grąžą. Todėl labai patartina investuotojams, ypač investuotojams, kurie nenori rizikuoti, įvertinti ir palyginti įvairių obligacijų trukmę, kad būtų pasiektas minimalus dispersijų derinys ir pritraukta maksimali grąža su kuo mažesne rizika. Be to, prieš priimant sprendimą pirkti reikia atsižvelgti į palūkanų normos faktorių.








