Neigiamos koreliacijos apibrėžimas
Žodžiu, neigiama koreliacija yra dviejų kintamųjų ryšys. Jie yra funkcijos, kurioje priklausomi ir nepriklausomi kintamieji vertės prasme juda skirtingomis kryptimis, dalis. Pavyzdžiui, jei nepriklausomas kintamasis didėja, priklausomas kintamasis mažėja ir atvirkščiai.
Neigiamą koreliaciją galima apibūdinti koreliacijos koeficientu, kai šios koreliacijos vertė yra nuo 0 iki -1. Tobulos neigiamos koreliacijos suma yra -1. Koreliacijos tarp kintamųjų stiprumas gali skirtis. Pavyzdžiui, tarkime, kad du kintamieji, x ir y koreliuoja -0,8. Tai reiškia, kad x padidėjus 1 vienetu, y sumažės 0,8. Dabar apsvarstykite, kad neigiama šių kintamųjų koreliacija yra -0,1. Tokiu atveju kiekvienas kintamasis x kintamojo vertės pokytis lems 0,1 vieneto skirtumą tik nuo kintamojo y kainos.
Neigiamos koreliacijos supratimas
Kad geriau suprastume neigiamą koreliaciją, turime gerai suprasti ir koreliaciją. Koreliacija yra statistinė priemonė, kuri yra dviejų skirtingų funkcijų ryšio laipsnio matas. Pavyzdžiui, žmogaus svoris ir ūgis. Paprastai, didėjant ūgiui, didėja ir žmogaus vertė. Tai rodo, kad yra teigiama koreliacija tarp ūgio ir svorio, nes didėjant vienam kintamajam, didėja ir kiti kintamieji. Tačiau koreliacija yra neigiama, jei du kintamieji juda priešingomis kryptimis, pavyzdžiui, aukščiu nuo sandariklio lygio ir temperatūra. Didėjant aukščiui, temperatūra mažėja.
Formulė pateikia koreliaciją:

Čia
- r = koreliacijos koeficientas;
- = X kintamojo vidurkis;
- = Y kintamojo vidurkis
Pertvarkymas suteikia mums šią formulę:

Koreliacija gali būti bet kokia reikšmė nuo -1 iki 1. Neigiamas ženklas rodo neigiamą koreliaciją, o teigiamas ženklas rodo teigiamą koreliaciją. Nulinė koreliacija reiškia, kad nėra ryšio tarp dviejų kintamųjų.

Kodėl neigiama koreliacija yra svarbi?
- Portfelio valdymas : Koreliacija plačiai naudojama valdant portfelius. Dažnai sakoma, kad portfeliai turėtų būti įvairūs. Ją turėtų sudaryti kelios investicijos, susijusios su skirtinga rizika ir grąža. Jei mūsų portfelyje yra tos pačios rūšies vertybiniai popieriai, bet kuris svarbus įvykis paveiks ne tik vieną vertybinį popierių, bet ir visą portfelį. Tuo tikslu randame koreliaciją tarp vertybinių popierių grąžos. Indėlių su visiškai teigiamomis koreliacijomis nereikėtų pirkti kartu. Norint diversifikuoti portfelį, dažnai pridedami statymai su neigiama koreliacija. Apsvarstykite aukščiau aptartą aviakompanijų akcijų ir naftos kainų pavyzdį. Jei portfelis turi energijos atsargų, vadovybė gali apsvarstyti galimybę pirkti aviakompanijų akcijas, kad apsisaugotų nuo naftos kainų kritimo.
- Ekonomika : Daugelis su ekonomika susijusių tendencijų sieja neigiamą koreliaciją. Šis judėjimų santykis gali būti naudingas sprendžiant su ekonomine politika susijusius klausimus. Pavyzdžiui, nedarbas ir vartotojų išlaidos. Kalbant apie išlaidų didėjimą, nedarbas mažėja (paprastai).
Realaus gyvenimo neigiamos koreliacijos pavyzdžiai
- Naftos kainos ir aviakompanijų atsargos: nafta yra pagrindinė žaliava aviakompanijoms. Didėjant naftos kainoms, jų pelningumas pradeda mažėti, o tai atsispindi ir jų akcijų kainose. Vadinasi, jie rodo neigiamą koreliaciją
- Akcijų rinka ir aukso kainos (dažniausiai, ne visada): Auksas visada veikia kaip alternatyvus investavimo būdas akcijų investuotojams. Taigi, kai tik vertybinių popierių rinka mažėja, investuotojai susidomi investuoti į auksą ir aukso kainos pradeda didėti
Praktinis neigiamos koreliacijos pavyzdys
Tarkime, kad 2011–2016 m. Laikotarpiu dvi atsargos kasmet teikė tokią grąžą:

Pirmosios atsargos grąžą laikant kintamuoju „x“, o antrosios - „y“.
Kintamojo xy apskaičiavimas
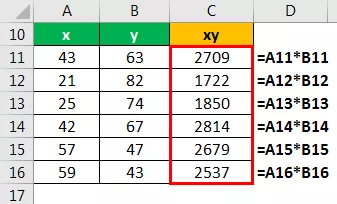
Kintamojo X 2 apskaičiavimas

Kintamojo Y 2 apskaičiavimas

Suma

Koreliacijos koeficiento (r) apskaičiavimas

- = ((6 * 14311) - (247 * 376)) / (((6 * 11409) - (247 2)) 0,5 * ((6 * 247160- (376 2)) 0,5)
- = Koreliacijos koeficientas (r) = -0,97608
Išsamų skaičiavimą rasite aukščiau pateiktame „Excel“ lape.
Neigiama koreliacijos koeficiento reikšmė rodo, kad kintamieji yra neigiamai koreliuojami.
Išvada
Kartais gali būti kitų veiksnių, dėl kurių kintamieji elgiasi tam tikru būdu. Aukščiau aptartame pavyzdyje galima daryti išvadą, kad kai x didėja, y mažėja. Tačiau bus neteisinga manyti, kad dėl „x“ padidėjimo „y“ sumažėja, nes gali būti, kad abi susijusios įmonės užsiima visiškai skirtingais verslais ir joms įtakos turi skirtingos ekonominės sąlygos.
Taigi koreliacijos turėtų būti naudojamos tik nustatant priežastį. Vadovai gali ją naudoti, kad suprastų santykį tarp kintamųjų, tokių kaip rinkos paklausa ir vartotojų išlaidos, kuris jau egzistuoja kaip analizės dalis. Tačiau jis neturėtų būti naudojamas tiriant vieno kintamojo pokyčius dėl kitų kintamųjų, nes visada bus keli veiksniai, darantys įtaką šiam ryšiui. Pavyzdžiui, vartotojų išlaidos rinkoje ir FMCG bendrovės pajamos. Jie gali parodyti teigiamą koreliaciją, tačiau gali būti, kad tos įmonės pajamos padidėjo dėl kokių nors kitų priežasčių, tokių kaip naujo produkto pristatymas ar plėtra į kylančios ekonomikos šalis.








