Koks yra koreliacijos koeficientas?
Koreliacijos koeficientas naudojamas nustatyti, koks stiprus yra santykis tarp dviejų kintamųjų, o jo vertės gali svyruoti nuo -1,0 iki 1,0, kur -1,0 reiškia neigiamą koreliaciją, o +1,0 - teigiamą ryšį. Jis atsižvelgia į santykinius kintamųjų judesius ir tada nustato, ar tarp jų yra ryšys.
Koreliacijos koeficiento formulė
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Kur
- r = koreliacijos koeficientas
- n = stebėjimų skaičius
- x = 1 g kintamasis kontekste
- Y = 2 -oji kintamasis
Paaiškinimas
Jei yra koks nors ryšys arba sakoma, kad ryšys tarp dviejų kintamųjų, tada jis nurodo, ar vienas iš kintamųjų keičiasi verte, tada kitas kintamasis taip pat linkęs keistis verte, tarkim, konkrečiai, kuris gali būti tas pats arba priešinga kryptimi. Skaičiuojamoji lygties dalis atlieka kartu judančių kintamųjų bandymą ir santykinį stiprumą, o lygties vardiklio dalis skaitiklį skaito, padaugindama kintamųjų skirtumus nuo kvadratinių kintamųjų.
Pavyzdžiai
1 pavyzdys
Apsvarstykite šiuos du kintamuosius: x ir y. Jums reikia apskaičiuoti koreliacijos koeficientą.
Žemiau pateikiami skaičiavimo duomenys.

Sprendimas:
Naudodami aukščiau pateiktą lygtį, galime apskaičiuoti tai

Mes turime visas aukščiau pateiktoje lentelėje pateiktas reikšmes, kai n = 4.
Dabar įveskime reikšmes koreliacijos koeficientui apskaičiuoti.

Todėl apskaičiuojama taip,

r = (4 * 25 032,24) - (262,55 * 317,31) / √ ((4 * 20 855,74) - (262,55) 2 ) * ((4 * 30 058,55) - (317,31) 2 )
r = 16 820,21 / 16 831,57
Koeficientas bus -

Koeficientas = 0,99932640
2 pavyzdys
X šalis yra augančios ekonomikos šalis, ir ji nori atlikti nepriklausomą centrinio banko priimtų sprendimų, susijusių su palūkanų normos pokyčiais, analizę, ar tai turėjo įtakos infliacijai ir ar centrinis bankas galėtų tą patį kontroliuoti.
Toliau pateikiama palūkanų normos ir infliacijos, vyraujančios šalyje vidutiniškai tais metais, santrauka.
Žemiau pateikiami skaičiavimo duomenys.

Šalies prezidentas kreipėsi į jus, kad atliktumėte analizę ir pateiktumėte pranešimą apie tą patį kitame susitikime. Naudokite koreliaciją ir nustatykite, ar centrinis bankas pasiekė savo tikslą.
Sprendimas:
Naudodami aukščiau aptartą formulę, galime apskaičiuoti koreliacijos koeficientą. Palūkanų normą traktuoti kaip vieną kintamąjį, sakykime x, o infliacijos lygį laikyti kitu kintamuoju kaip y.

Mes turime visas aukščiau pateiktoje lentelėje pateiktas reikšmes, kai n = 6.
Dabar įveskime reikšmes koreliacijos koeficientui apskaičiuoti.


r = (6 * 170,91) - (46,35 * 22,24) / √ ((6 * 361,19) - (46,35) 2 ) * ((6 * 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Koreliacija bus -

Koreliacija = -0,92
Analizė: Panašu, kad koreliacija tarp palūkanų normos ir infliacijos yra neigiama, o tai atrodo teisingas ryšys. Didėjant palūkanų normai, infliacija mažėja, o tai reiškia, kad jos linkusios judėti viena priešinga kryptimi, ir iš aukščiau pateikto rezultato matyti, kad centriniam bankui pavyko įgyvendinti sprendimą, susijusį su palūkanų normų politika.
3 pavyzdys
ABC laboratorija atlieka ūgio ir amžiaus tyrimus ir norėjo sužinoti, ar tarp jų yra ryšys. Jie surinko 1000 žmonių atranką kiekvienai kategorijai ir sugalvojo vidutinį ūgį toje grupėje.
Žemiau pateikiami duomenys koreliacijos koeficientui apskaičiuoti.

Jūs turite apskaičiuoti koreliacijos koeficientą ir padaryti išvadą, kad jei yra koks nors ryšys.
Sprendimas:
Amžių traktuoti kaip vieną kintamąjį, sakykime x, o ūgį (cm) laikyti kitu kintamuoju kaip y.

Mes turime visas aukščiau pateiktoje lentelėje pateiktas reikšmes, kai n = 6.
Dabar įveskime reikšmes koreliacijos koeficientui apskaičiuoti.

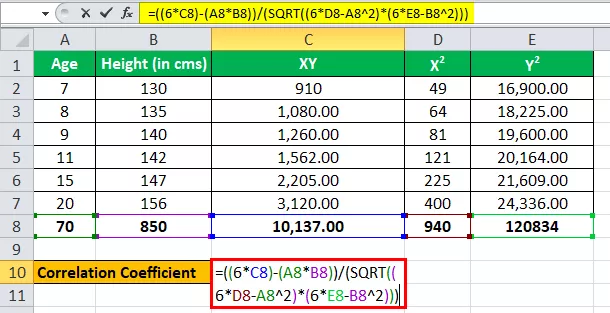
r = (6 * 10 137) - (70 * 850) / √ ((6 * 940 - (70) 2 ) * ((6 * 1,20,834) - (850) 2 )
r = 1 322,00 / 1 361,23
Koreliacija bus -

Koreliacija = 0,971177099
Aktualumas ir naudojimas
Statistikoje jis naudojamas daugiausia analizuojant santykio tarp nagrinėjamų kintamųjų stiprumą, be to, taip pat matuojama, ar tarp pateiktų duomenų rinkinių yra koks nors tiesinis ryšys ir kaip gerai jie galėtų būti susiję. Viena iš įprastų koreliacijoje naudojamų priemonių yra Pirsono koreliacijos koeficientas.
Jei kintamasis keičiasi verte ir kartu su kitu kintamuoju, keičiasi vertė, tada suprasti tą ryšį yra labai svarbu, nes galima panaudoti pirmojo kintamojo vertę, kad būtų galima numatyti pastarojo kintamojo vertės pokytį. Šiuo šiuolaikiniu laikotarpiu koreliacija turi daugybę būdų, pavyzdžiui, naudojama finansų pramonėje, moksliniuose tyrimuose ir kur ne. Tačiau svarbu žinoti, kad koreliacija turi tris pagrindinius santykių tipus. Pirmasis yra teigiamas ryšys, kuriame teigiama, kad pasikeis kintamojo vertė, tada pasikeis ir susijęs kintamasis ta pačia kryptimi. Panašiai, jei yra neigiamas ryšys, susijęs kintamasis elgsis priešingai. Be to, jei nėra koreliacijos, tada r reikš nulinę vertę.Norėdami geriau suprasti sąvoką, žiūrėkite toliau pateiktus vaizdus.