Sudėtinis apibrėžimas
Palūkanų normos apskaičiavimo metodas yra palūkanos už palūkanas, kai apskaičiuojamos palūkanos už investiciją / pradinę pagrindinę dalį, pridėjus uždirbtas palūkanas ir kitas reinvesticijas, kitaip tariant, uždirbtos palūkanos kaupiamos iki pagrindinės sumos, priklausomai nuo indėlio ar paskolos laikotarpio. tai gali būti kas mėnesį, kas ketvirtį ar kasmet
Pabandykime suprasti kelis pagrindinius pavyzdžius ir tai, kas yra sudėtinga ir kaip tai veikia
4 populiariausi jungimo galios pavyzdžiai
1 pavyzdys
Shane'as ir Markas abu nusprendė investuoti 1 000 000 USD, tačiau Shane'as nusprendė investuoti į paprastas palūkanas, o Markas dešimt metų investuoja į sudėtines palūkanas su 10% palūkanomis. Pažiūrėkime, kas nutiks po dešimties metų.
Sprendimas:
Taigi, Shane investicijų apskaičiavimas bus -

Bendra uždarbio suma = 200 000 USD
Su paprastu palūkanomis Shane'as po 10 metų gaus 2 000 000 USD.
Investicijos į markę bus apskaičiuotos taip:

Bendra uždarbio suma = 2,59,374 USD
Su sudėtinėmis palūkanomis Marko investicijų vertė išaugs iki 2 599 374 USD.
Dabar Shane'as nusprendė investuoti taikydamas tokius sudėtinius metodus kaip Markas, ir jie abu investavo 2 000 000 USD 15% tarifu.
Shane investicijos bus apskaičiuotos taip:

Bendra uždarbio suma = 8,09,111,55 USD
Shane lieka investuota 10 metų ir gauna galutinę sumą kaip 8,09,111,55 USD, taikant 15% normą.
Investicijos į markę bus apskaičiuotos taip:

Bendra uždarbio suma = 65,83,790,52 USD
Tačiau Markas yra kantrūs ilgalaikiai investuotojai ir investuoja 25 metus, o jo investicinė vertė išauga iki 65,83 790,52 USD
Aukščiau pateiktame pavyzdyje parodyta jungimo galia. Kuo ilgesnis investicijų horizontas, tuo didesnis yra eksponentinis augimas.
2 pavyzdys (kas savaitę)
Simonas turi 7500 USD santaupų, o sūnaus kolegijos fondui, kuris ketina lankyti kolegiją po 15 metų, jis nusprendė investuoti į JAV taupomąsias obligacijas. Simono tikslas yra sutaupyti 20 000 USD, o JAV taupymo obligacijų metinė procentinė norma yra 6%. Kokia būsima Simono pinigų vertė po 15 metų?
Sprendimas:
Atsižvelgiant į tai,
- Pagrindinis = 7500 USD
- Norma = 6% arba 0,06
- Laikotarpis = 15 metų.
- Kiek kartų jis padidėja per metus n = 52 savaitės
- Ateities vertė =?
Taigi būsimos vertės apskaičiavimas bus -

Savaitės sudėjimo formulė yra tokia, kaip nurodyta toliau.
F = P (1 + r / n) n * t- F = 7500 USD (1 + 0,06 / 52) 52 * 15
- F = 7500 USD (1 + 0,001153846) 780
- F = 18 437,45 USD
Taigi iš aukščiau pateikto skaičiavimo aišku, kad Simono tikslas sutaupyti 20,00 USD nebus pasiektas aukščiau nurodytais metodais, tačiau jis arčiau to.
Nuolatinio sujungimo metodas
Dabar pabandykime pirmiau pateiktą pavyzdį su tęstinio formavimo formule.
Taigi būsimos vertės apskaičiavimas bus -

- F = 7500 USD 0,06 * 15
- F = 7500 USD 0,9
- Ateities vertė (F) = 18 447,02 USD
Dabar, net ir naudojant „Continound Compounding“, nebus pasiektas Simono tikslas sutaupyti 20 000 USD sūnaus kolegijos fondui.
Pažiūrėkime su „Mėnesio sudėtine formule“, kiek pinigų Simonas turėjo investuoti, kad pasiektų savo tikslą - sutaupyti 20 000 USD per 15 metų, kai jo metinė norma yra 6%?
Taigi būsimos vertės apskaičiavimas bus -
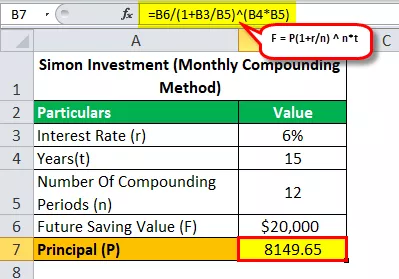
- 20 000 USD = P (1 + 0,06 / 12) 12 * 15
- P = 20 000 USD / (1 + 0,06 / 12) 12 * 15
- Pagrindinis (P) = 8149,65
Taigi, išsprendę aukščiau pateiktą lygtį, gausime atsakymą, kuris yra 8 149,65 USD (suma, kurią Simonas turi investuoti, kad pasiektų tikslą sutaupyti 20 000 USD per 15 metų).
3 pavyzdys (faktinis metinis pajamingumas)
Tarkime, ribotas XYZ bankas senjorams už fiksuotą indėlį per metus skiria 10 proc. Lėšų, o mes čia darome prielaidą, kad banko palūkanos kas ketvirtį didinamos kaip ir visi kiti bankai. Apskaičiuokite faktinį metinį pajamingumą 5, 7 ir 10 metų.
Sprendimas:
Metinis pajamingumas 5 metams:
- t = 5 metai
- n = 4 (susidedama kas ketvirtį)
- I = 10% per metus
Taigi A = (1 + 10% / 100/4) (5 * 4)
- A = (1 + 0,025) 20
- A = 1.6386
- Aš = 0,6386 per 5 metus
Efektyvios palūkanos = 0,6386 / 5
Efektyvus I = 12,772% per metus
Metinis pajamingumas 7 metams:
- t = 7 metai
- n = 4 (susidedama kas ketvirtį)
- I = 10% per metus
Taigi A = (1 + 10% / 100/4) (7 * 4)
- A = (1 + 0,025) 28
- A = 1,9965
- Aš = 1,9965 per 7 metus
- Efektyvus I = 0,9965 / 7
Efektyvus I = 14,236% per metus
Metinis pajamingumas 10 metų:
- t = 10 metų
- n = 4 (susidedama kas ketvirtį)
- I = 10% per metus
Taigi A = (1 + 10% / 100/4) (10 * 4)
- A = (1 + 0,025) 40
- A = 2,685
- I = 1.685 per 10 metų
- Efektyvus I = 1.685 / 10
Efektyvus I = 16,85% per metus
4 pavyzdys - (anuitetai: būsima vertė)
Kas 3 mėnesius investuojama po 1000 USD, kasmet mokant po 4,8% per metus. Kiek bus verta anuitetas per 10 metų?
Sprendimas:
Taigi, kai sakome, kiek anuitetas bus vertas per 10 metų, tai reiškia, kad turime rasti būsimą vertę, ir tai yra svarbu, nes kai tik yra anuitetų pavyzdys, turime pamatyti, ką turime sužinoti.
Taigi, Ateities vertės formulė yra
Anuiteto FV = P ((1+ r) n - 1 / r)- P = periodinis mokėjimas
- r = laikotarpio norma
- n = laikotarpių skaičius
Taigi Ateities vertės formulė yra
- Taigi čia P = 1000 USD
- r = 4,8% per metus arba 0,048
- r (kas ketvirtį) = 0,048 / 4
- r (kas ketvirtį) = 0,012
- n = 10 metų
- n (sudėties kartų skaičius) = 10 × 4 = 40
Taigi, anuiteto FV apskaičiavimas bus -

Taigi dabar FV = 1000 USD (1 + 0,012) 40 -1 / 0,012)
Taigi, išsprendę aukščiau pateiktą lygtį, gausite 50 955,30 USD FV
Taigi, kiek bus anuitetas per 10 metų ir atsakymas yra 50 955,30 USD
Be to, iš pirmiau pateikto pavyzdžio taip pat galime sužinoti, kiek palūkanų uždirbama per 10 metų.
Investuojama 40 kartų 1000 USD, tai yra bendra investicija (40 × 1000 USD = 40 000 USD).
Taigi palūkanos = būsima vertė - bendra investicija
- Palūkanos = 50 955,30 USD - 40 000 USD
- Palūkanos = 10 955,30 USD
Taigi čia svarbu suprasti, kad anuitetuose investuotojai gali sulaukti didelio susidomėjimo. Pirmiau pateiktuose pavyzdžiuose už 40 000 USD indėlį mainais gaunamos visos 10 955,30 USD palūkanos.
Pastaba: Norėdami atsisiųsti išsamiau, galite atsisiųsti aukščiau pateiktą „Excel“ šabloną.








