Kas yra diapazono formulė?
Diapazono formulė reiškia formulę, kuri naudojama apskaičiuojant skirtumą tarp didžiausios ir mažiausios diapazono vertės, o pagal formulę mažiausia vertė atimama iš didžiausios vertės, norint nustatyti diapazoną.
Diapazonas = didžiausia vertė - mažiausia reikšmė
Iš pateikto duomenų rinkinio, kuris statistikams ir matematikams geriau supranta duomenų rinkinį, koks jis yra įvairus. Tai paprasčiausias būdas apskaičiuoti statistikos dispersiją.
Paaiškinimas
Tai gana paprasta ir paprasta naudoti, nes formulėje nurodoma jo maksimali vertė, atėmus minimalią nurodyto mėginio vertę. Todėl didžiausios ir mažiausios vertės dispersija yra diapazonas, ir, nors tai paprasta naudoti ir suprasti, ją reikia tinkamai interpretuoti.
Pvz., Jei duomenyse yra kontūrininkas, diapazonui tai darytų įtaką ir gautų rezultatą, kuris suklaidintų. Paimkite praktinį pateiktų duomenų 2, 4, 7, 7, 100 pavyzdį, tada diapazonas būtų 100 - 2, tai yra 98, tačiau, kaip matome, duomenų diapazonas yra mažesnis nei 10, tačiau atsižvelgiant ir aiškinant, kad duomenys yra 98 sukels klaidingą informaciją. Todėl diapazonas turėtų būti aiškinamas tinkamai.
Pavyzdžiai
1 pavyzdys
Apsvarstykite pateiktą duomenų rinkinį 2,2,4,4, 4, 6,7,7,8, 8, 8, 9, 9, 9, 9, 9. Jūs turite apskaičiuoti šios imties diapazoną.
Sprendimas:
- Didžiausia vertė = 9
- Minimali vertė = 2
Diapazonas = 9 - 2
Diapazonas = 7
2 pavyzdys
Ponas Starkas, mokslininkas, 10 metų dirbantis kompanijoje „Dream moon“. Ponas Arora, jo vadovas, vykdo eksperimentą su žmonių sveikata ir surinko keletą pavyzdžių, susijusių su vyrų ūgiu, kurie yra 162, 158, 189, 144, 151, 150, 151, 178, 155, 160. Dabar jis yra suglumęs ir nori žinoti, kiek duomenų yra įvairių. Ponas Starkas, kuris yra patyręs statistikas, kreipėsi į jo vadovą poną Arorą, kad pašalintų painiavą dėl formulės variacijos. Ponas Arora privalo pateikti atsakymą savo vadovui; jūs turite apskaičiuoti, kiek skiriasi duomenys?
Sprendimas:
Diapazonas = didžiausia vertė - mažiausia vertė
- Didžiausia vertė = 189
- Minimali vertė = 144
Diapazonas = 189 - 144
Diapazonas = 45
Surinktų duomenų ar imties variacija yra 45.
3 pavyzdys
Ponas Buffetas, gerai žinomas ir gerbiamas investuotojas visame pasaulyje, dabar svarsto JAV rinkos akcijas ir analizuoja keletą jų, kur nori investuoti. Sąraše yra pagrindinės JAV „blue-chip“ kompanijos. Žemiau yra pateiktos pasirinktos akcijos ar vertybiniai popieriai kartu su naujausia jų akcijų rinkos kaina, kuri žymima JAV doleriais, kur jis svarsto galimybę investuoti.
Privalote apskaičiuoti diapazoną ir pateikti sąrašo variantą.
Sprendimas:
Žemiau pateikiami diapazono apskaičiavimo duomenys.
Naudojant aukščiau pateiktą informaciją, „Max“ vertė „Excel“ bus apskaičiuojama taip:

Maksimali vertė = 204,66
Min. „Excel“ vertės apskaičiavimas taip:
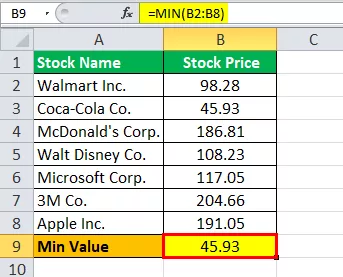
Min. Vertė = 45,93
Todėl diapazonas apskaičiuojamas taip,

Diapazonas = 204,66–45,93
Asortimentas bus -
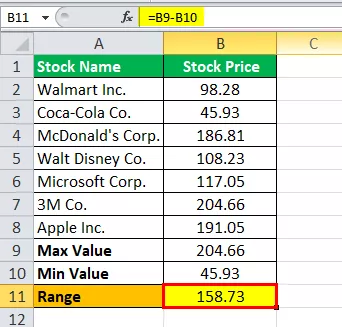
Diapazonas = 158,73
Diapazono formulės naudojimas
Diapazonas savaip yra labai paprastas ir labai paprastas suprasti, kaip pasiskirsto skaičiai duotame duomenų rinkinyje arba tam tikroje imtyje, nes, kaip minėta anksčiau, apskaičiuoti yra palyginti lengva, nes yra reikalaujama tik iš labai paprastos aritmetinės operacijos, kuri tik atima minimumą iš didžiausios vertės, tačiau diapazone ji turi dar keletą programų tam tikram duomenų rinkiniui ar tam tikrai statistikos imčiai. Diapazonas taip pat naudingas vertinant kitą plitimo matą, kuris vadinamas dispersija arba standartiniu nuokrypiu.
Diapazonas, kaip minėta anksčiau, gali suteikti informacijos tik apie pagrindinę informaciją, ty apie tai, kur pasklis tam tikros imties ar pateikto duomenų rinkinio sklaida. Suteikiant skirtumą arba sakant dispersiją tarp didžiausios ir mažiausios tam tikros imties ar nurodyto duomenų rinkinio reikšmių, gaunama viena informacija arba apytikslė idėja apie reikšmingus kraštutinius pastebėjimus, kiek tai yra plačiai paplitę, tačiau vėlgi tai neduoda jokios informacijos užuomina ar bet kokia informacija apie kitus duomenų taškus, kur jie gulėtų, o tai yra pagrindinis diapazono lygties naudojimo trūkumas.
Diapazonas, kaip aptarta aukščiau, yra naudingas vaizduojant pasklidimą tam tikroje imtyje arba tam tikrame duomenų rinkinyje, be to, jis taip pat naudojamas lyginant gautą skirtumą tarp tos pačios pateiktos imties ar tų pačių nurodytų duomenų rinkinių.








