Paprasta taupymo skaičiuoklė
Paprasto taupymo skaičiuoklė gali būti naudojama apskaičiuojant termino sumą, kuri turi būti prieinama asmeniui, kuriame jis turi galimybių investuoti, ir jis pasirinks, kur jis gali padidinti savo grąžą.
Paprasta taupymo skaičiuoklė
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
Kur- Aš - pradinė investuota suma.
- r yra palūkanų norma.
- n yra laikotarpių, už kuriuos reikia sutaupyti, skaičius.
- F yra mokamų palūkanų dažnis
- i yra fiksuota suma, investuota reguliariais intervalais.
Apie paprastą taupymo skaičiuoklę
Formulė yra tokia, kaip nurodyta toliau:
Matematiškai jį galima apskaičiuoti vienkartinėms paprastoms santaupoms:
M = I * (1 + r / F) n * FAntra, jei kas mėnesį sutaupoma paprasta, apskaičiuojama:
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1 / r)Kur
- M yra visa suma paprastojo taupymo laikotarpio pabaigoje
- Aš - pradinė investuota suma
- i yra fiksuota suma, investuota reguliariais intervalais
- r yra palūkanų norma
- F yra mokamų palūkanų dažnis
- n yra laikotarpių, už kuriuos reikia sutaupyti, skaičius.
Yra daugybė bankų ir kitų finansų įstaigų, kurios konkuruoja rinkoje, norėdamos pritraukti indėlius, kad galėtų užsiimti daugiau verslu, ty skolinti pinigus įmonėms ar didelės grynosios vertės asmenims. Kai kurie bankai mokėtų didesnę palūkanų normą, jei indėliai viršytų tam tikrus ribinius limitus ir būtų laikomi sąskaitoje, priešingu atveju jie mokės standartinę palūkanų normą. Be to, gali skirtis palūkanų išmokėjimo dažnumas; pavyzdžiui, palūkanos gali būti didinamos ir mokamos kas ketvirtį, pusmetį arba kasmet, priklausomai nuo banko. Todėl naudodamiesi šia skaičiuokle, asmenys galėtų nustatyti, kurią finansų įstaigą jie turėtų pasirinkti investuoti savo pinigus, palygindami pagrindinės sumos grąžinimo terminą ar grąžą.
Kaip apskaičiuoti paprastą santaupą?
Norint apskaičiuoti paprastą santaupą, reikia atlikti šiuos veiksmus.
1 žingsnis - nustatykite, kokia suma būtų investuota, nesvarbu, ar ji yra vienkartinė, ar yra periodinė investicija, tada į tą patį reikėtų atsižvelgti ir skaičiuojant taupymo normas.
2 žingsnis - išsiaiškinkite palūkanų normą, kuri yra prieinama pasirinktinai asmeniui, ir kuri būtų uždirbta arba tikimasi uždirbti iš paprastų santaupų.
3 žingsnis. Dabar nustatykite laikotarpį, kuriam jis bus investuotas, ir daugiausia tai bus ilgalaikis laikotarpis ir priklausys nuo kiekvieno atvejo.
4 žingsnis - padalykite palūkanų normą iš laikotarpių, už kuriuos mokamos palūkanos arba paprastosios santaupos, skaičiaus. Pavyzdžiui, jei mokama norma yra 5% ir ji mokama kas mėnesį, tada palūkanų norma būtų 5% / 12, tai yra 0,416%.
5 žingsnis. Dabar naudokite formulę, kuri buvo aptarta pirmiau 1 punkte), jei paprastos santaupos yra vienkartinės, ir naudokite 2 formulę), jei paprastų santaupų suma atliekama reguliariais intervalais, kartu su bet kokia pradine visų turimų parinkčių suma .
6 žingsnis - gautas skaičius bus termino suma, į kurią taip pat bus įskaičiuotos paprastųjų santaupų pajamos ir pasirinkta ta, kurios palūkanos bus didžiausios.
Paprasto taupymo skaičiuoklės pavyzdys
Ponas Williamas dabar yra suaugęs ir džiaugiasi atidaręs savo pirmąją taupomąją sąskaitą. Jis ieškojo finansų įstaigos, kuri teikia dideles palūkanas, tačiau yra sumišęs, nes negauna, kuris bankas jam duos didžiausią grąžą. Žemiau yra citatos, kurias ponas Williamas įtraukė į sąrašą.

Jis nori investuoti 1500 USD į bet kurią iš sąskaitų ir investuos taip, kaip sąskaita moka palūkanas. Pavyzdžiui, jei bankas moka pusmetį, tada kiekvieno laikotarpio pabaigoje suma bus investuojama vienodai ir tai bus daroma 10 metų.
Remdamiesi pateikta informacija, turite apskaičiuoti sumą, kurią jis sutaupytų, ir už jas uždirbtas palūkanas bei į kurį banką jis turėtų investuoti.
Sprendimas:
Mums pateikiama ši išsami informacija:
I BANKAS
- I = pradinė suma bus lygi nuliui
- r = palūkanų norma, kuri yra 3,00%, o kas ketvirtį bus 3,00% / 4, tai yra 0,75%
- N = čia kas ketvirtį rodomas dažnis; taigi tai bus 4
- n = paprastųjų taupymo metų skaičius, kuris čia yra 10 metų.
- i = tai įprasta investuotina suma, kuri yra 1500/4, ty 375 USD

Dabar, norėdami apskaičiuoti termino sumą, galime naudoti žemiau pateiktą formulę.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
- = 0 * (1 + 0,75%) 10 * 4 + 375 * ((1 + 0,75%) 10 * 4 - 1 / 0,75%)
- = 17 417,43
Termino suma bus 17 417,43
Uždirbtos sudedamosios palūkanos būtų 17 417,43 USD - 375 * 40 USD = 2417,43 USD.

II BANKAS
- I = pradinė suma bus lygi nuliui
- r = palūkanų norma, kuri yra 3,12%, o kas pusmetį bus 3,12% / 2, tai yra 1,56%.
- N = dažnis, kuris čia yra kas pusmetį, taigi jis bus 2
- n = paprastųjų taupymo metų skaičius, kuris čia yra 10 metų.
- i = tai įprasta investuoti suma, kuri yra 1500/2, tai yra 750 USD

Dabar, norėdami apskaičiuoti termino sumą, galime naudoti žemiau pateiktą formulę.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1 / r)
- = 0 * (1 + 1,56%) 10 * 2 + 750 * ((1 + 1,56%) 10 * 2 - 1) / 1,56%
- = 17 445,58 USD
Termino vertė bus 17 445,58 USD
Uždirbtos bendros palūkanos būtų 17 445,58 USD - (750 USD * 20) = 2445,58 USD.

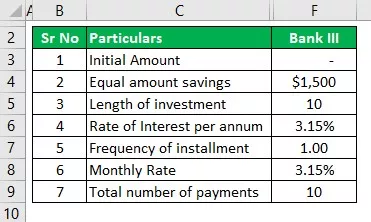
III BANKAS
- I = pradinė suma bus lygi nuliui
- r = palūkanų norma, kuri yra 3,15%, ir kasmet bus 3,15% / 1, tai yra 3,15%
- N = čia kasmet rodomas dažnis, taigi jis bus 1
- n = paprastųjų taupymo metų skaičius, kuris čia yra 10 metų.
- i = tai įprasta investuoti suma, kuri yra 1500/1, tai yra 1500 USD
Dabar, norėdami apskaičiuoti termino sumą, galime naudoti žemiau pateiktą formulę.
M = I * (1 + r) n * F + i * ((1 + r) n * F - 1) / r
- = 0 * (1 + 3,15%) 10 * 1 + 1500 * ((1 + 3,15%) 10 * 1 - 1) / 3,15%
- = 17 315,08 USD
Termino suma bus 17 315,08 USD
Uždirbtos bendros palūkanos būtų 17 315,08 USD - (1500 USD * 10) = 2315,08 USD.

Didžiausia uždirbta suma yra II banke, todėl jis turėtų atidaryti sąskaitą II banke.

Išvada
Šią skaičiuoklę, kaip aptarta aukščiau, galima naudoti norint palyginti skirtingas finansų įstaigos terminų sumas, nes didesnė palūkanų norma negarantuoja didžiausios absoliučios sumos, kaip parodyta aukščiau pateiktame pavyzdyje. Taigi reikėtų apskaičiuoti ir palyginti sumas pagal terminą ir tada priimti sprendimą.








