„Chi Square“ testas „Excel“ Kaip atlikti Chi kvadrato testą su pavyzdžiu

Turinys

„Chi-Square“ testas naudojant „Excel“

„Chi-Square“ testas naudojant „Excel“

„Chi-Square test in excel“ yra dažniausiai naudojamas neparametrinis testas, naudojamas norint palyginti du ar daugiau atsitiktinai parinktų duomenų kintamųjų. Tai yra tam tikro tipo testas, naudojamas norint sužinoti santykį tarp dviejų ar daugiau kintamųjų, jis naudojamas statistikoje, kuris taip pat žinomas kaip „Chi-Square P“ reikšmė. formulės, skirtos atlikti chi kvadrato testą, naudojant matematinę chi kvadrato testo formulę.

Tipai

„Chi-Square“ tinkamumo testas
„Chi-Square“ dviejų kintamųjų nepriklausomumo testas.

1 - „Chi-Square“ tinkamumo testas

Jis naudojamas imant populiacijai tinkamo mėginio artumą. „Chi-Square“ testo simbolis yra (2). Tai yra visų ( Stebėtų skaičių - Laukiamų skaičių) ² / Laukiamų skaičių suma.

Kur k-1 laisvės laipsniai arba DF.
Kur Oi yra stebimas dažnis, k yra kategorija, o Ei - numatomas dažnis.

Pastaba: - Statistinio modelio tinkamumas reiškia supratimą, kaip atrinkti duomenys tinka stebėjimų rinkiniui.

Naudoja

Skolininkų kreditingumas pagal jų amžiaus grupes ir asmenines paskolas
Ryšys tarp pardavėjų darbo rezultatų ir gautų mokymų
Vienų akcijų ir tokio sektoriaus, kaip farmacijos ar bankininkystės, grąža
Žiūrovų kategorija ir TV kampanijos poveikis.

# 2 - dviejų kintamųjų nepriklausomumo testas „Chi-Square“

Jis naudojamas norint patikrinti, ar kintamieji yra vienas nuo kito autonomiški, ar ne. Su (r-1) (c-1) laisvės laipsniais

Kur Oi yra stebimas dažnis, r yra eilučių skaičius, c yra stulpelių skaičius, o Ei - numatomas dažnis

Pastaba: - Du atsitiktiniai kintamieji vadinami nepriklausomais, jei vienas kintamojo tikimybės pasiskirstymo neveikia kito.

Naudoja

Nepriklausomybės testas tinka šioms situacijoms:

Yra vienas kategorinis kintamasis.
Yra du kategoriniai kintamieji, kuriuos turėsite nustatyti tarp jų.
Yra kryžminės lentelės, todėl reikia rasti ryšį tarp dviejų kategorinių kintamųjų.
Yra kiekybiškai neįvertinamų kintamųjų (pavyzdžiui, atsakymai į klausimus, pavyzdžiui, ar skirtingų amžiaus grupių darbuotojai renkasi skirtingus sveikatos planų tipus?)

Kaip atlikti „Chi-Square“ testą programoje „Excel“? (su pavyzdžiu)

Restorano vadovas nori rasti ryšį tarp klientų pasitenkinimo ir žmonių, laukiančių stalų, atlyginimų. Tuo mes nustatysime hipotezę, kad išbandytume Či aikštę

Ji ima atsitiktinę 100 klientų imtį, klausdama, ar aptarnavimas buvo puikus, geras ar prastas.
Tada ji laukiančių žmonių atlyginimus skirsto į mažus, vidutinius ir didelius.
Tarkime, kad reikšmingumo lygis yra 0,05. Čia H0 ir H1 žymi paslaugų kokybės nepriklausomumą ir priklausomybę nuo laukiančių stalų žmonių atlyginimų.
H ₀ - paslaugų kokybė nepriklauso nuo stalų laukiančių žmonių atlyginimų.
H ₁ - paslaugų kokybė priklauso nuo žmonių, laukiančių stalų, atlyginimų.
Jos išvados pateiktos žemiau esančioje lentelėje:

Čia mes turime 9 duomenų taškus, turime 3 grupes, kurių kiekviena gavo skirtingą pranešimą apie atlyginimą, o rezultatas pateiktas žemiau.

Dabar mes suskaičiuosime visų eilučių ir stulpelių sumą. Tai atliksime naudodami formulę, ty SUM. Norėdami iš viso stulpelio Išskirti puikų, parašėme = SUM (B4: D4) ir paspauskite klavišą Enter.

Tai suteiks mums 26 . Mes atliksime tą patį su visomis eilutėmis ir stulpeliais.

Norėdami apskaičiuoti laisvės laipsnį (DF), mes naudojame (r-1) (c-1)

DF = (3-1) (3-1) = 2 * 2 = 4

Yra 3 paslaugų kategorijos ir 3 atlyginimų kategorijos.
Turime 27 respondentus, kurių atlyginimas vidutinis (apatinė eilutė, vidurinė)
Mes turime 51 respondentą su gera paslauga (paskutinis stulpelis, vidurys)

Dabar turime apskaičiuoti numatomus dažnius: -

Laukiamus dažnius galima apskaičiuoti pagal formulę: -

Norėdami apskaičiuoti „ Excellent“, naudosime „ Low “ sumą padauginę iš „ Excellent “ sumos, padalytos iš N.

Tarkime, kad turime apskaičiuoti 1-ą eilutę ir 1-ą stulpelį (= B7 * E4 / B9 ) . Tai suteiks numatomą klientų, kurie balsavo už puikų aptarnavimą, laukiančių žmonių atlyginimų skaičius bus mažas, ty 8,32 .

E _{11 =} - (32 * 26) / 100 = 8,32 , E ₁₂ = 7,02 , E ₁₃ = 10,66
E ₂₁ = 16,32 , E ₂₂ = 13,77 , E ₂₃ = 20,91
E ₃₁ = 7,36 , E ₃₂ = 6,21 , E ₃₃ = 9,41

Panašiai ir mes visi turime daryti tą patį, o formulė taikoma žemiau esančioje diagramoje.

Gauname laukiamo dažnio lentelę, kaip nurodyta toliau: -

Pastaba: - Tarkime, kad reikšmingumo lygis yra 0,05. Čia H0 ir H1 žymi paslaugų kokybės nepriklausomumą ir priklausomybę nuo laukiančių stalų žmonių atlyginimų.

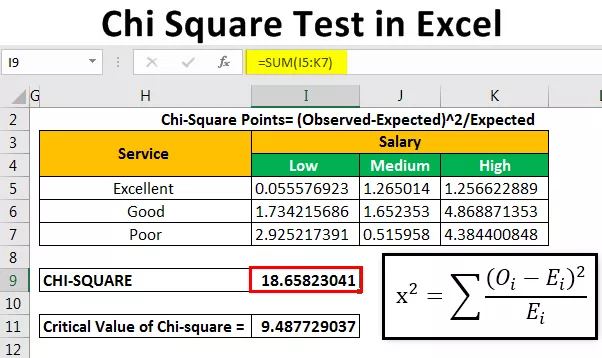
Apskaičiavę laukiamą dažnį, naudodami formulę apskaičiuosime chi kvadrato duomenų taškus.

Chi kvadrato taškai = (pastebėta-tikėtasi) 2 / tikėtasi

Norėdami apskaičiuoti pirmąjį tašką, parašome = (B4-B14) 2 / B14.

Nukopijuosime ir įklijuosime formulę į kitus langelius, kad vertė būtų automatiškai užpildyta.

Po to mes apskaičiuosime chi vertę (apskaičiuotą vertę) , pridėdami visas vertes, pateiktas virš lentelės.

„Chi“ vertę gavome kaip 18,65823 .

Norėdami apskaičiuoti kritinę vertę, mes naudojame chi kvadrato kritinių verčių lentelę, kurioje galime naudoti toliau pateiktą formulę.

Šioje formulėje yra 2 parametrai CHISQ.INV.RT (tikimybė, laisvės laipsnis).

Tikimybė yra 0,05, ir tai yra reikšminga reikšmė, kuri padės mums nustatyti, ar priimti Null hipotezę (H ₀ ), ar ne.

Kritinė chi kvadrato vertė yra 9,487729037.

Dabar rasime chi kvadrato vertę arba (P reikšmę) = CHITEST (faktinis_diapazonas, numatomas_diapazonas)

Diapazonas nuo = CHITEST (B4: D6, B14: D16) .

Kaip matėme, chi testo arba P vertės reikšmė yra = 0,00091723.

Mes apskaičiavome visas vertes. Į chi kvadrato (skaičiuojama vertė) vertės yra tik reikšmingas, kai jos vertė yra tokia pati ar daugiau nei kritinę vertę 9.48, ty kritinė reikšmė (lentelėse vertė) turi būti didesnė nei 18.65 priimti nulinė hipotezė (H ₀ ) .

Bet čia apskaičiuota vertė > lentelė

X ² (apskaičiuota)> X ² (lentelėje)

18.65> 9.48

Tokiu atveju mes atmesime Null hipotezę (H ₀ ) ir bus priimta alternatyvioji (H ₁ ) .

Mes taip pat galime naudoti P reikšmę tam pačiam nuspėti, ty jei P vertė <= α (reikšminga reikšmė 0,05), Null hipotezė bus atmesta.
Jei P reikšmė> α , neatmeskite nulinės hipotezės .

Čia P reikšmė (0,0009172) < α (0,05), atmeskite H ₀ , priimkite H ₁

Iš aukščiau pateikto pavyzdžio darome išvadą, kad paslaugų kokybė priklauso nuo laukiančių žmonių atlyginimų.

Ką reikia atsiminti

Mano, kad kvadratas yra įprastas normalus variantas.
Įvertina, ar skirtingose kategorijose pastebėti dažniai labai skiriasi nuo numatytų prielaidų rinkinių.
Nustato, kaip tariamai paskirstymas atitinka duomenis.
Naudojamos nenumatytų atvejų lentelės (atliekant rinkos tyrimus šios lentelės vadinamos kryžminiais skirtukais).
Jis palaiko vardinio lygio matavimus.